
R programming language) define them so that they have plus signs instead. In the equation, following the convention introduced by Box and Jenkins. Moving average parameters (θ’s ) are defined so that their signs are negative
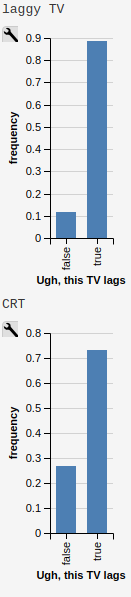
#Eon timer lag series#
Rather, it is the first-difference-of-the-first difference, which is the discreteĪnalog of a second derivative, i.e., the local acceleration of the series (the d=2 case) is not the difference from 2 periods ago. The forecasting equation is constructed as follows. q is the number of lagged forecast errors in the prediction.d is the number of nonseasonal differences needed for.p is the number of autoregressive terms,.Nonseasonal ARIMA model is classified as an "ARIMA(p,d,q)" model, Random-trend models, autoregressive models, and exponential smoothing models "integrated" version of a stationary series. Which needs to be differenced to be made stationary is said to be an Lags of the stationarized series in theįorecasting equation are called "autoregressive" terms, lags of theįorecast errors are called "moving average" terms, and a time series Optimization methods (“hill-climbing”) rather than by just solving Include lagged errors must be estimated by nonlinear With using lagged errors as predictors is that the model’s predictions are not linear functions of theĬoefficients, even though they are linear functions of the past data.

Is no way to specify “last period’s error” as an independentĬomputed on a period-to-period basis when the model is fitted to the data. The errors, an ARIMA model it is NOT a linear regression model, because there Period (LAG(Y,1) in Statgraphics or Y_LAG1 in RegressIt). Regression model in which the independent variable is just Y lagged by one Regression model and which could be fitted with standard regressionįirst-order autoregressive (“AR(1)”) model for Y is a simple (“self-regressed”) model, which is just a special case of a Predictors consist only of lagged values of Y, it is a pure autoregressive Recent values of Y and/or a weighted sum of one or more recent values of Predicted value of Y = a constant and/or a weighted sum of one or more Signal is then extrapolated into the future to obtain forecasts.įorecasting equation for a stationary time series is a linear (i.e., regression-type) equation in which the predictors “filter” that tries to separate the signal from the noise, and the Sign, and it could also have a seasonal component. Of signal and noise, and the signal (if one is apparent) could be a pattern ofįast or slow mean reversion, or sinusoidal oscillation, or rapid alternation in A random variable of this form can be viewed (as usual) as a combination (correlations with its own prior deviations from the mean) remain constant over The latter condition means that its autocorrelations Its variations around its mean have a constant amplitude, and it wiggles in aĬonsistent fashion, i.e., its short-term random time patterns always look Random variable that is a time series is stationary if its statistical With nonlinear transformations such as logging or deflating (if necessary). “stationary” by differencing (if necessary), perhaps in conjunction Models for forecasting a time series which can be made to be
Forecasting equation: ARIMA models are, in theory, the most general class of


 0 kommentar(er)
0 kommentar(er)
